УДК 621.73

НАПРЯЖЕНИЯ ГОРЯЧЕГО МЕТАЛЛА ОТ ДЕФОРМАЦИЙ ПРИ КОВКЕ

Антощенков Ю.М.

Электростальский политехнический институт филиал МГИСиС, г. Электросталь, Московская обл., ул. Первомайская 7

E-mail: dekanat@elektrostal.ru

Аннотация

Дается связь тензора напряжений от деформаций при основных операциях ковки с учетом теплового состояния металла заготовки, учитывается деформационный разогрев и приводятся конкретные результаты расчета.

Ключевые слова: напряжение, ковка, температура, слитки.

За последние годы в технологии машиностроения на стадии получения заготовок и деталей резко возросла доля процессов обработки металлов давлением (ОМД). Это связано с тем, что ОМД обеспечивает высокое качество металла заготовок, существенное снижение расхода металла и повышение производительности труда.

Придание металлу необходимой формы, возможно ближе, отвечающей конфигурации будущей детали и получаемой с наименьшими трудозатратами; исправление дефектов литой структуры; повышение качества металла преобразованием литой структуры в деформированную; распределение свойств металла в объеме поковки по закону, удовлетворяющему эксплуатации данной детали на стадии изготовления пластическим деформированием и, наконец, сама возможность пластического деформирования малопластичных сплавов – основные аргументы применения процессов обработки металлов давлением.

Улучшения качества металла достигают не только при его выплавке, разливке и последующей термической обработке, но и в процессе ОМД. Даже самые совершенные в настоящее время процессы плавки и электрошлаковый переплав металла, глубокое вакуумирование плавки и перед разливкой не обеспечивают наивысшего качества металла, полного ресурса его деформационных и прочностных характеристик.

Вот почему такое большое внимание уделяется сейчас целенаправленному применению высокопроизводительных и экономичных процессов ОМД в технологии машиностроения.

Из всего многообразия процессов обработки металлов давлением наиболее универсальна ковка. Только ковкой можно получить и крупные многотонные деформированные изделия и поковки массой несколько десятков грамм.

Задачи изучения пластического течения металла, деформационной способности металлов занимает большое место как в теории ОМД, так и в научном обосновании протекающих и оснополагающих процессов ковки. При этом решение практических задач методом скольжения позволяет сочетать физические предпосылки с высокой математической точностью, особенно, когда, когда при пластическом деформировании заготовки встречаются множество разнохарактерных зон деформаций, и аналитические расчеты становятся громоздкими. В настоящее время метод линий скольжения – это единственный метод, позволяющий анализировать распределение напряжений по сечению тела.

Учитывая в дальнейшем влияние термозональных факторов при горячем деформировании и упрочнение металла, приближает этот метод к реальным условиям деформирования металла заготовок, что дает возможность наблюдения за динамическим поведением металла в очагах деформаций, оценивать напряженное и деформированное состояния металла, отыскивать наиболее оптимальные технологические параметры ковки и прогнозировать свойства деформированного металла.

Большое место в обработке металлов давлением занимает исследование деформационной способности металлов и прежде всего способности к обработке в горячем состоянии, разработка методов оценки предельной пластичности на основе напряженного состояния металла с учётом тепловых факторов деформирования заготовки в нагретом состоянии.

На всем протяжение ковки нагретой заготовки её состояние включает несколько этапов, которые определяют тепловой цикл ковки.

  1. Технологические особенности теплового цикла ковки

    Термическое воздействие на металл поковок в процессе ковки на каждом промежутке технологического цикла получения качественного металла характеризуется не однозначно.

    Если за начало этого цикла принять состояние металла слитков после нагрева перед транспортировкой к деформирующему оборудованию (завершение рекристаллизационного процесса), а окончание - поковка на складе готовой продукции, то в кузнечном цехе этот цикл включает следующие этапы:

    - Нагрев металла заготовок, в том числе и нагрев с горячего посада слитков;

    - транспортировка нагретой заготовки к деформирующему оборудованию, вплоть до контакта технологического инструмента с поверхностью заготовки при холостом ходе деформирующего инструмента;

    - период непосредственной деформации заготовки (неоднозначное термическое воздействие:

    - охлаждение металла за счет излучения, конвективных процессов, теплопроводности при контакте с инструментом,

    - деформационный разогрев за счет диссипации части механической энергии пластического деформирования и работы контактных и внутренних сил трения);

    - охлаждение металла поковок после ковки (не включая период промежуточной термообработки).

    При этом возможны непредусмотренные отклонения от данного термического цикла, существенно не влияющие на свойства металла в рамках ТУ на изделие, но тем не менее изменяющие температурные условия нагретой заготовки:

    - теплообмен при захвате манипуляторами (небольшие поверхности контакта и небольшой период времени контакта при транспортировке заготовки);

    - нагрев металла за счет работы контактных сил трения, когда большая часть выделяющийся тепловой энергии уходит в более холодный инструмент и существенного влияния на изменение температуры заготовки не оказывает. Поэтому не существенные факторы при постановке тепловой задачи не учитывались или упрощались.

  2. Расчет теплового поля исходной заготовки.

Для оценки температурного поля заготовки в процессе термического цикла ковки использовали известное дифференциальное уравнение теплопроводности:

(1.1)

где:

r (Т) - плотность металла поковки;

с(Т) - теплоемкость металла поковки;

l (Т) - коэффициент теплопроводности.

При этом приняли, что выделение и распределение тепловой энергии в результате деформации, равномерно;

на стадии деформирования заготовки изменение деформационных, энергосиловых и теплофизических характеристик учитывается дискретно, считая, что в данный момент и в данном объеме металла вышеуказанные характеристики постоянны.

Краевые условия для уравнения 1.1 с учетом технологических особенностей термического цикла ковки следующие:

1). Начальное распределение температуры приняли соответствующему параболическому закону:

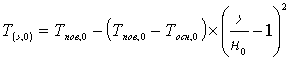, (1.2)

где:Тпов,0 - температура поверхности заготовки в начальный момент времени;

Тосн,0 - температура центральной части заготовки ( геометрическая продольная ось симметрии);

Н0 - половина толщены полосы или радиус среднего диаметра заготовки;

х - текущая координата.

 

2). Граничные условия при транспортировке нагретой заготовки от нагревательных печей к деформирующему оборудованию:

а) На поверхности заготовки:

(1.3)

где: s 0 - коэффициент излучения абсолютно-черного тела;

e n - степень черноты поверхности заготовки ( для нагретого металла, имеющего на поверхности слой окислов (окалины) e n=0,8);

Тср - температура окружающей среды;

Тпов - температура поверхности металла.

Для определения a к при обтекании заготовки потоком воздуха, использовали критериальное уравнение теплообмена:

, (1.4)

 

где:

- критерий Нусильта;

- критерий Рейнольдса;

l возд.- коэффициент теплопроводности воздуха при температуре окружающей среды;

n возд. - вязкость воздуха при температуре окружающей среды.

После подставления в уравнение (1.4) выражений для соответствующих критерий получили формулу для определения a к:

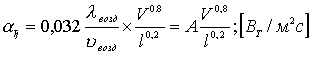, (1.5)

где:

    1. скорость движения слитка;

l - теплоотводящая длина заготовки.

Коэффициент А зависит от температуры окружающей среды ( при 200 С, А= 5,04).

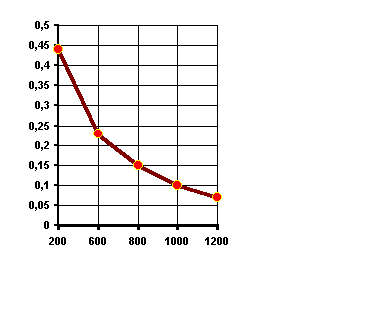
Влияние конвекционного механизма теплопередачи с ростом температуры поверхности заготовки уменьшается (Рис.1.1) и при температурах 12000 С и выше доля конвективного теплообмена не превышает 5-7%, и им в дальнейших расчетах пренебрегаем.

a к /a

Т, оС

Рис. 1.1. Доля конвенции в общей теплопередачи с поверхности заготовки (V = 3 м/с; l = 5м).

 

а). На оси заготовки:

(1.6)

При решении данной тепловой задачи использовали метод конечной разности. Шаг разбиения по пространственной координате составляет:

где: n - число слоев разбивки поперечного сечения слитка.

Шаг разбиения по координате времени, исходя из условия обеспечения устойчивости решения (условие сходимости):

где:

k - коэффициент температуропроводности металла

заготовки.

Заменяя частные производные в уравнении теплопроводности (1.1) на их конечные разности, получили:

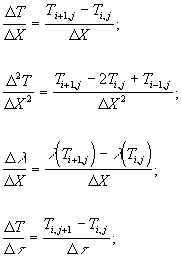(1.7)

где: i - номер поперечного слоя сечения, i=1,2,3...n;

j - номер интервала времени, j=1,2,3...m.

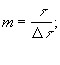- число интервалов разбиения по координате времени;

t - время охлаждения (нагрева) металла.

Подставляя полученные уравнения в выражение теплопроводности и после преобразований получили уравнение температуры заготовки в каждый последующий момент времени:

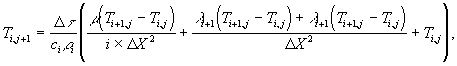(1.8)

Таким образом, зная распределение температуры для j - го интервала времени, используя уравнение (1.8) нашли распределение температуры в ( i+1) – и в j момент времени и так далее.

Для оценки поверхностного и центрального слоев заготовки ввели дополнительные (фиктивные) слои, которые находятся на расстоянии D C от поверхности и от её оси. Температура фиктивного поверхностного слоя для граничного условия описывается уравнением (1.3) и определяется исходя из выражения:

(1.9)

где: a - коэффициент теплопроводности с поверхности заготовки;

Тср - температура окружающей среды.

Температура фиктивного слоя в близи оси заготовки для граничного условия, описываемого уравнением (1.6) определяется как:

(1.10)

Температура на поверхности или оси заготовки определяется, как среднее арифметическое значение температур поверхностного или осевого слоев фиктивных слоев. Все это позволяет учитывать изменение теплофизических характеристик металла (с, r , l ) от температуры слоя, что позволяет добиться более точных результатов.

Предварительные расчеты и экспериментальные результаты показывают, поверхность заготовки при перемещении (расстояние транспортировки определяется нормами компоновки оборудования технологического процесса) её от печи до деформирующего оборудования охлаждается незначительно, в пределах 50-700С для углеродистых сталей и средних по массе слитков. При этом температура центра практически не изменяется. Перепад температур по сечению в период транспортировки заготовки невелик и как следствие возникающие термические напряжения малы, и в дальнейшем при расчетах учитываться не будут.

Термический цикл деформации заготовки. Этот период характеризуется неоднозначными условиями термического воздействия на металл поскольку деформация металла при ковке дискретна (обжатие - отдых в период холостого хода инструмента). В период холостого хода заготовка только остывает. В период деформации с учетом технологических особенностей процесса ковки одновременно и остывает и нагревается за счет деформационного разогрева металла (яркий пример этого “ковочные кресты” поперечного сечения).

При соприкосновения технологического инструмента с заготовкой (начало обжатия) - точка отчета термического цикла в период деформации. Тогда t = 0 и температура в любой точке рассматриваемого тела зависит только от двух переменных: координаты Х и времени t . При этом уравнение теплопроводности примет вид:

(1.11)

где: k - коэффициент теплопроводности.

При этом краевые условия данного этапа выглядят, как:

Начальные условия:

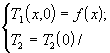(1.12)

Граничные условия:

(1.13)

где: l 1,2 - коэффициент, учитывающий условия теплообмена между поверхностью заготовки и инструментом при наличие промежуточного слоя в виде окалины.

В результате решения уравнений (1.11-1.13) получили следующие распределение температуры для заготовки:

(1.14)

где:

h - приведенный коэффициент теплопроводности;

b1 и b2 - коэффициенты, характеризующие

тепловую активность соответственно металла

заготовки и инструмента ().

Сопоставив это решение с решением краевой задачи для полубесконечного тела с граничными условиями III рода с нашими выражением температурной задачей:

(1.15).

Получили возможность привести наши условия к решению более простой задачи, заключающийся в охлаждении только одной заготовки, но для следующих условий:

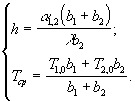(1.16).

 

Учет деформационного разогрева заготовки при ковке. Теплота, выделяющиеся в результате диссипации механической работы пластической деформации, величина которой может определена как:

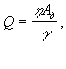(1.17)

где: h - коэффициент выхода тепла при пластической деформации (h =0,84-0,94);

g - механический эквивалент теплоты;

Ад - работа пластической деформации, которая зависит от интенсивности деформации сдвига Г и интенсивности касательных напряжений Т в данной точке объекта деформации:

(1.18)

где:

Т - интенсивность касательных напряжений, среднее значение которого для эдиальных условий составляет:

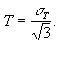(1.19)

Разбивая процесс деформирования на ряд коротких интервалов D t , стремящихся к нулю, и в которых деформацию можно считать малой и следовательно однородной, предположим, что для углеродистых сталей и им подобным с большой теплопроводностью и при сравнительно небольшой скорости деформации, выделяющаяся теплота будет распределяться равномерно по всему объёму заготовки. Тогда изменение температуры за счет деформационного разогрева составит:

(1.20)

где: m - масса металла в очаге деформации.

Поскольку в данном периоде термического цикла проходит одновременно охлаждение металла (падение температуры ранее нагретой заготовки) и деформационный разогрев (подъём температуры), то итоговое изменение температуры составит:

(1.20)

где: D Тдеф. - интервал температуры разогрева металла;

D Т - температурный интервал охлаждения в данный момент интервала времени.

Принимая температуру в формулах, предложенных Соколовским В.В., равной суммарной величина термических напряжений составит:

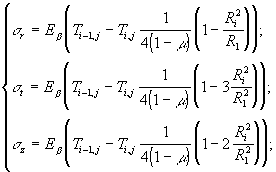(1.21)

где: s r - радиальное напряжение;

s t - тангенциальное напряжение;

s z - напряжение в осевом направлении;

Eb - модуль упругости;

b - коэффициент линейного расширение;

m - коэффициент Пуассона для пластической деформации;

Ri - расстояние от i-го слоя до оси заготовки;

R1 - радиус заготовки (половина высоты полосы);

Ti,j - температура в данном слое и в данный момент времени.

Анализ обжатия плоскими бойками со средней величиной деформации 10% слитка массой 5 тонн из стали 45, показал заметное увеличение температуры металла по всему сечению заготовки за счет деформационного разогрева (рис. 1.2).

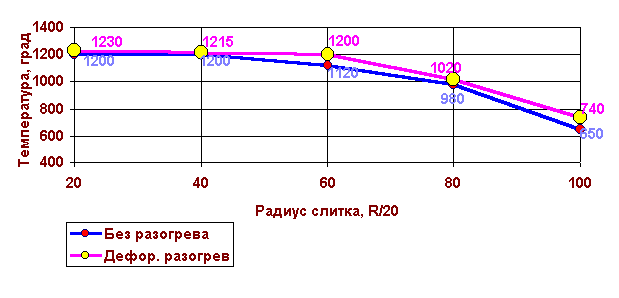
Рис. 1.2. Распределение температуры по сечению слитка

Коррекция координатных систем напряжений и тепловых полей. Координатная система, принятая при определении деформационных напряжений, отличается от координатной системы при расчете термических напряжений. Решение совместной деформационной и термической задачи требует коррекцию этих систем с целью приведения их в единую.

Принимали, что при корректировке координаты деформационных напряжений будут базовыми. Координаты, величина и направление термических напряжений корректируются исходя из следующего:

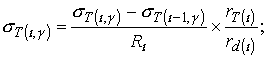(1.22)

где: величина термических напряжений в смежных слоях;

- номинальный радиус вектор координат деформационных напряжений;

- радиус-вектор i - го слоя координат соответственно термических и деформационных напряжений.

Изменение термозональных факторов слитка в процессе нагрева и последующей деформации существенно сказывается на напряженноe состояние металла, повышая сжимающие напряжения при снижении величены растягивающих нормальных напряжений. При этом величина тангенциальных напряжений практически остается без изменений. На рисунках 1.3, 1,4 представлены эпюры расчетных напряжений при единичном обжатие плоскими бойками (e ср= 10%) слитка массой 5 тонн из стали 45, температура начало ковки 12000С.

Распределение в поперечном сечении средних нормальных напряжений, рассчитанные на ЭВМ с использованием пакета прикладных программ,

где: эпюра напряжений а)- , б) -, с) - .

Рис. 1.3. Напряженное состояние металла в очаге деформаций

 

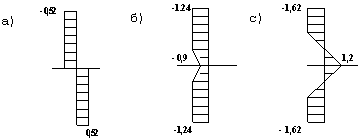
где: эпюра напряжений а)- , б) -, с) - .

Рис. 1.4. Напряженное состояние металла в очаге деформации с учетом деформационного разогрева металла

 

разработанные на основе данного метода расчета ковки с учетом теплового поля очага деформаций, представлены на рис. 1.5. Условие деформаций, температурное состояние заготовки, схемы ковки и граничные условия для данных расчетов остались прежними, что использовались в предыдущих расчетах.

 

Рис. 1.5. Распределение средних нормальных напряжений по сечению слитка при единичном обжатии плоскими бойками

 

ВЫВОДЫ ПО ГЛАВЕ

1. Деформационный разогрев металла в пластическом очаге деформации повышает уровень средних нормальных напряжений от центра очага к его периферии, при этом уровень тангенциальных напряжений практически остается без изменений.

2. Распределение нормальных напряжений при деформационном разогреве жарактерезуется снижением их к центру оси заготовки и при небольших деформациях до 5% возможно изменение начальной схемы напряженного состояния с появлением растягивающих напряжений в центральной зоне заготовки.

3. Выявлено, что для заготовок из углеродистых сталей за счет дополнительных термических напряжений возможна пластическая деформация до величины показателя степени деформации 3%.

 

*                   *                   *

ДИСКУССИЯ

От кого Вопрос Ответ
   

 

Задать вопрос

Вопрос
(комментарии)
Подпись
Ваш e-mail

Желательно заполнять все поля формы